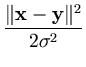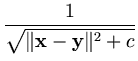


Next: 3. Mixture of local
Up: 2.4 Kernel PCA
Previous: 2.4.2 Centering in feature
2.4.3 Common kernel functions
The kernel function needs to be a scalar product in some feature space. A sufficient condition is that the kernel matrix is positive semidefinite (Schölkopf et al., 1998b; Schölkopf and Smola, 2002, p. 44). Some common kernel functions that fulfill this condition are the polynomial kernel,
with a constant integer d, the Gaussian kernel,
with a constant
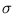 > 0, and the inverse multiquadric kernel,
> 0, and the inverse multiquadric kernel,
with a constant c > 0 (Schölkopf and Smola, 2002, p. 54). The last two functions result in a kernel matrix with full rank (Micchelli, 1986). That is, all eigenvectors are linearly independent. Thus, the dimensionality of the feature space is not restricted (it is infinite).



Next: 3. Mixture of local
Up: 2.4 Kernel PCA
Previous: 2.4.2 Centering in feature
Heiko Hoffmann
2005-03-22