


Next: 2.4.1 Feature extraction
Up: 2. Modeling of data
Previous: 2.3.2 Mixture of probabilistic
2.4 Kernel PCA
Different from the mixture models, kernel PCA (Schölkopf et al., 1998b) just works with a single PCA. It is an extension of PCA to non-linear distributions. Instead of directly doing a PCA, the n data points 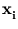 are mapped into a higher-dimensional (possibly infinite-dimensional) feature space,
are mapped into a higher-dimensional (possibly infinite-dimensional) feature space,
As it turns out later, the computation of this mapping can be omitted. In the feature space, principal components are extracted. That is, the following equation needs to be solved (here, we first assume that
{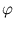 (
(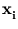 )} has zero mean, see section 2.4.2):
)} has zero mean, see section 2.4.2):
with the covariance matrix
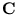 =
= 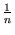
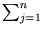
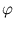 (
(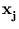 )
)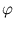 (
(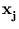 )T. From the definition of
)T. From the definition of 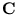 follows that
follows that
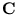
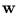 is a linear combination of the vectors
is a linear combination of the vectors
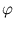 (
(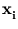 ). Thus,
). Thus, 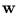 must lie in the span of
must lie in the span of
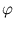 (
(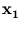 ),...,
),...,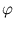 (
(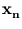 ). Hence, we can write
). Hence, we can write
Combining (2.23) and (2.24) gives
which is equivalent to the set of n equations
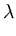 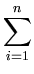 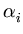 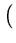 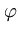 ( (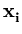 )T )T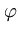 ( (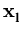 ) )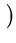 = = 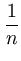 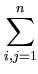 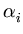 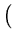 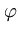 ( (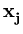 )T )T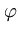 ( (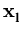 ) )  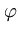 ( (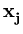 )T )T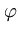 ( (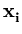 ) )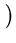 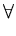 l . l . |
(2.26) |
The direction from (2.26) to (2.25) is fulfilled because the left side of (2.25) is in the span of
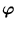 (
(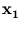 ),...,
),...,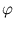 (
(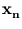 ), and (2.26) defines all
n projections on
), and (2.26) defines all
n projections on
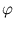 (
(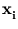 ). Equation (2.26) has the favorable property that it is written entirely with scalar products in the feature space. Hence, we do not need to carry out the transformation
). Equation (2.26) has the favorable property that it is written entirely with scalar products in the feature space. Hence, we do not need to carry out the transformation
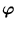 , which would be computationally impossible for an infinite-dimensional feature space. It is enough to work in the original space. Thus, instead of working with the scalar product
, which would be computationally impossible for an infinite-dimensional feature space. It is enough to work in the original space. Thus, instead of working with the scalar product
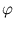 (
(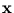 )T
)T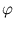 (
(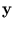 ), we are
only working with a kernel function
k(
), we are
only working with a kernel function
k(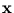 ,
,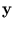 ) =
) = 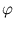 (
(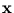 )T
)T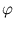 (
(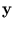 ). For the given data points, this function can be
written as a matrix
). For the given data points, this function can be
written as a matrix 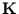 , with
Kij = k(
, with
Kij = k(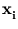 ,
,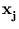 ). Using the
kernel matrix, (2.26) can be written as
). Using the
kernel matrix, (2.26) can be written as
with
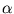 = (
= (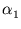 ,...,
,...,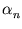 )T. As shown in appendix C.2, (2.27) is equivalent to
)T. As shown in appendix C.2, (2.27) is equivalent to
Thus, the vector
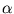 for each principal component can be obtained by extracting the eigenvectors of
for each principal component can be obtained by extracting the eigenvectors of 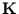 . For further processing, the principal component
. For further processing, the principal component 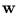 needs to be normalized to have unit length. This can be also established by working solely with the kernel,
needs to be normalized to have unit length. This can be also established by working solely with the kernel,
||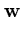 ||2 = ||2 = 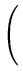 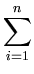 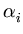 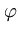 ( (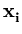 ) )  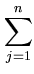 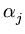 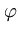 ( (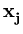 ) )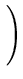 = = 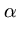 T T 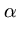 = n = n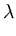 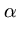 T T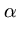 , , |
(2.29) |
which results in a normalization rule for
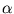 .
.
To apply kernel PCA, a data point's features (the projections on the principal components) need to be extracted, and the formalism needs to be adjusted to distributions that do not have zero mean in feature space. These two points are addressed in the following sections. Furthermore, a short list of common kernel functions is given.
Subsections



Next: 2.4.1 Feature extraction
Up: 2. Modeling of data
Previous: 2.3.2 Mixture of probabilistic
Heiko Hoffmann
2005-03-22
![]() are mapped into a higher-dimensional (possibly infinite-dimensional) feature space,
are mapped into a higher-dimensional (possibly infinite-dimensional) feature space,