4.5.2 Results

The abstract RNN could cope with the redundant arm postures for a given end-effector position; the MLP could not (table 4.3). The local PCA mixture approximated the training data also better then Neural Gas (table 4.3). The results from the different mixture models NGPCA, NGPCA-constV, and MPPCA-ext were almost equal (table 4.3). Compared to NGPCA, NGPCA-constV was slightly worse on the inverse direction. Over five different training cycles (retraining of the mixture of local PCA), the average position errors varied only slightly (for NGPCA, the maximum deviation was 2 mm).

Table 4.3: Position and collision errors for an abstract RNN using NGPCA, NGPCA-constV, and MPPCA-ext for training, compared to a variant using Neural Gas for training and to a multilayer perceptron (MLP). Results are shown for two different directions of recall: forward and inverse. The inverse model takes the desired collision state as an additional input variable (third column). Position errors are averaged over all test patterns, and are given with standard deviations. In the inverse case, the collision error is the percentage of trials deviating from the collision input value. In the forward case, it is the erroneous number of collision state predictions.

method	direction	input	position error (mm)	collision error (%)
NGPCA	inverse	no collision	27 ± 15	5
NGPCA	inverse	collision	23 ± 13	8
NGPCA	forward	-	44 ± 27	11
NGPCA-constV	inverse	no collision	31 ± 17	5
NGPCA-constV	inverse	collision	28 ± 14	11
NGPCA-constV	forward	-	43 ± 29	11
MPPCA-ext	inverse	no collision	29 ± 15	5
MPPCA-ext	inverse	collision	25 ± 14	6
MPPCA-ext	forward	-	45 ± 29	14
Neural Gas	inverse	no collision	58 ± 26	2
Neural Gas	inverse	collision	56 ± 27	4
Neural Gas	forward	-	160 ± 74	18
MLP	inverse	no collision	310 ± 111	30
MLP	forward	-	93 ± 48	13

The mixture models distribute the training patterns among the units of the mixture. For NGPCA and NGPCA-constV, every pattern is assigned to one unit (at the end of the training). The number of patterns assigned to a unit is a measure for the weight of the unit; for MPPCA-ext, the weights are the prior probabilities. These weights had roughly a bell-shaped distribution among the units (figure 4.10). Different from MPPCA-ext, the distributions for NGPCA and NGPCA-constV showed a second peak for units having few assigned patterns (around 50, the average is 250). A single peak seems to be favorable. However, the distribution of assigned patterns also depends on the structure of the data set (which is largely unknown). Apparently, in this experiment, the effect on the performance was negligible (table 4.3).

Figure 4.10: Histogram of assigned patterns, respective prior probabilities. n is the number of units for each interval.

The remaining tests were carried out only with NGPCA. The distribution of the individual errors shows regions corresponding to different ellipsoids selected during the recall (figure 4.11). At the transition between two regions, the error as a function of the input is discontinuous.

Figure: Position errors of the inverse model with input `collision'. (Left) Horizontal plane (approximately 70mm above the table). (Right) Vertical plane through the origin (z = 0).

The performance depends on the number of units m and principal components q. The position and the collision errors decreased with increasing m (table 4.4). Furthermore, the position error was smallest at q = 6 (figure 4.12, right). This q value matches the local dimensionality of the distribution (figure 4.12, left).

The abstract RNN could also cope with additional noise dimensions if the number of principal components was adjusted accordingly (table 4.5). With three noise dimensions and q = 6 principal components, the position errors of the abstract RNN were more than double . However, with q = 9, the position errors were again at the no-noise level.

Table 4.4: Dependence on the number m of units.

direction	input	error	m = 50	m = 100	m = 200
inverse	no collision	position (mm)	48	38	27
inverse	no collision	collision (%)	5	5	5
inverse	collision	position (mm)	47	35	23
inverse	collision	collision (%)	8	9	8
forward	-	position (mm)	74	56	44
forward	-	collision (%)	16	14	11

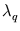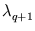Figure 4.12: (Left) Ratio of successive averaged eigenvalues $\lambda_{{q}}^{}$ and $\lambda_{{q+1}}^{}$ (see methods). (Right) Dependence of the position error E (here for the direction: inverse, no collision) on the number of principal components q.

Table 4.5: Compensation of noise. The first column of numbers shows the result without noise dimensions (as in table 4.3), the second with three noise dimensions and six principal components, and the third with noise and nine principal components.

direction	input	error	q = 6 (no noise)	q = 6	q = 9
inverse	no collision	position (mm)	27	57	30
inverse	no collision	collision (%)	5	6	6
inverse	collision	position (mm)	23	64	24
inverse	collision	collision (%)	8	6	11
forward	-	position (mm)	44	101	45
forward	-	collision (%)	11	15	13

The errors for the forward direction were consistently higher than for the inverse direction (table 4.3 and 4.4). The major difference seems to be that the forward direction has six input dimensions; the inverse direction has only four. This is consistent with the finding that the square error per output dimension increased with the number of input dimensions (figure 4.13). For intermediate numbers r, the increase was even exponential. In the following section, this finding is investigated theoretically.

Figure 4.13: Mean square error (SE) as a function of the number r of input dimensions. The dashed line is the function a exp(br) fitted to point 2 to 8; b was 0.59±0.03.