


Next: 2.1.1 Neural networks for
Up: 2. Modeling of data
Previous: 2. Modeling of data
2.1 Principal component analysis (PCA)
Principal component analysis is a widely used tool for dimension reduction (Diamantaras and Kung, 1996). Let
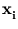
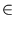 IRd, where
i = 1,..., n, be the training patterns. The principal components are a set of q < d orthonormal vectors and span a subspace in the major directions into which the patterns extend (figure 2.1).
IRd, where
i = 1,..., n, be the training patterns. The principal components are a set of q < d orthonormal vectors and span a subspace in the major directions into which the patterns extend (figure 2.1).
Figure 2.1:
The principal component 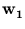 points into the direction of maximum variance. The gray dots are the training patterns. The intersection of the dashed lines is the center of the pattern distribution.
points into the direction of maximum variance. The gray dots are the training patterns. The intersection of the dashed lines is the center of the pattern distribution.
|
|
In this section, we assume that the patterns are centered around the origin (without loss of generality). Let 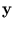 be the projection onto a subspace,
be the projection onto a subspace,
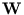 is a d×q matrix that contains the principal components as columns.
The vector
is a d×q matrix that contains the principal components as columns.
The vector 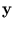 is a dimension-reduced representation of
is a dimension-reduced representation of 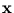 . Let
. Let
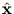 be the reconstruction of
be the reconstruction of 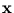 given only the vector
given only the vector 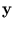 ,
,
The goal of PCA is to set the subspace such that the mean reconstruction error
Erec is minimized,
This goal is equivalent to finding the q major directions of maximal variance within the set of patterns
{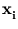 } (Diamantaras and Kung, 1996). Moreover, it is equivalent to the principal components being the first q eigenvectors
} (Diamantaras and Kung, 1996). Moreover, it is equivalent to the principal components being the first q eigenvectors 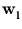 of the covariance matrix
of the covariance matrix 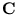 of the pattern set (Diamantaras and Kung, 1996),
of the pattern set (Diamantaras and Kung, 1996),
The corresponding eigenvalue equation is
The eigenvalue 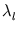 is the variance of the distribution
{
is the variance of the distribution
{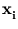 } in the direction of
} in the direction of 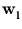 . The following sections describe how neural networks can extract principal components and how PCA can be linked to the probability density of a pattern distribution.
. The following sections describe how neural networks can extract principal components and how PCA can be linked to the probability density of a pattern distribution.
Subsections



Next: 2.1.1 Neural networks for
Up: 2. Modeling of data
Previous: 2. Modeling of data
Heiko Hoffmann
2005-03-22
![]()
![]() IRd, where
i = 1,..., n, be the training patterns. The principal components are a set of q < d orthonormal vectors and span a subspace in the major directions into which the patterns extend (figure 2.1).
IRd, where
i = 1,..., n, be the training patterns. The principal components are a set of q < d orthonormal vectors and span a subspace in the major directions into which the patterns extend (figure 2.1).
![\includegraphics[width=12cm]{pcavariance.eps}](img90.gif)
![]() be the projection onto a subspace,
be the projection onto a subspace,