


Next: 2.2 Vector quantization
Up: 2.1 Principal component analysis
Previous: 2.1.1 Neural networks for
2.1.2 Probabilistic PCA
Probabilistic PCA links PCA to the probability density of patterns 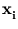 (Tipping and Bishop, 1997). The given set
{
(Tipping and Bishop, 1997). The given set
{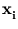 } is assumed to originate from a probability density
p(
} is assumed to originate from a probability density
p(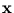 ). Further,
). Further, 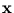 is assumed to be a linear combination of a vector
is assumed to be a linear combination of a vector
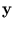
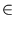 IRq with density
p(
IRq with density
p(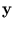 ) and a noise vector
) and a noise vector
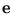
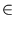 IRd with density
p(
IRd with density
p(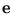 ),
),
The goal is to find 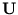 , which is a
d×q matrix. Both densities
p(
, which is a
d×q matrix. Both densities
p(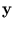 ) and
p(
) and
p(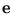 ) are assumed to be uniformly Gaussian with variance one respective
) are assumed to be uniformly Gaussian with variance one respective 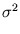 . Thus, the density
p(
. Thus, the density
p(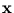 ) is defined uniquely up to the parameters
) is defined uniquely up to the parameters 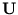 and
and 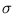 ,
,
p(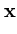 ) = (2 ) = (2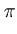 )-d/2(det )-d/2(det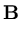 )-1/2exp )-1/2exp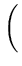 - - 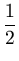 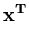 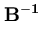 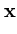  |
(2.8) |
with
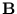 =
= 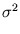
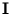 +
+ 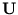
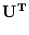 (Tipping and Bishop, 1997). Probabilistic PCA determines
(Tipping and Bishop, 1997). Probabilistic PCA determines 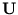 and
and 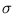 such that the patterns
such that the patterns 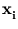 if drawn from
p(
if drawn from
p(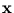 ) are most likely (Tipping and Bishop, 1997). That is, the likelihood, which is
) are most likely (Tipping and Bishop, 1997). That is, the likelihood, which is
L = 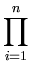 p( p(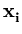 ) , ) , |
(2.9) |
is maximized (see appendix A.2 for an example of the maximum likelihood principle). The result of this optimization gives the matrix 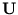 (Tipping and Bishop, 1997),
(Tipping and Bishop, 1997),
The columns of the matrix 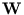 are the eigenvectors of the covariance matrix of
{
are the eigenvectors of the covariance matrix of
{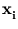 }; the diagonal matrix
}; the diagonal matrix
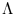 contains the corresponding eigenvalues, and
contains the corresponding eigenvalues, and 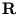 is an arbitrary rotational matrix (note,
is an arbitrary rotational matrix (note, 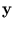 has a uniform Gaussian distribution). The noise variance
has a uniform Gaussian distribution). The noise variance 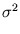 turns out to be the residual variance per dimension,
turns out to be the residual variance per dimension,
To evaluate (2.11), only the q principal eigenvalues and the total variance (sum of variances over all dimensions, which equals the trace of the covariance matrix) need to be known. It is not necessary to compute the d - q minor principal components. Thus, the introduction of the noise allows the density
p(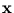 ) to be defined over the whole
IRd, while using a reduced parameter set (obtained by PCA). Equation (2.11) shows how fast
p(
) to be defined over the whole
IRd, while using a reduced parameter set (obtained by PCA). Equation (2.11) shows how fast
p(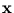 ) decreases orthogonal to the subspace spanned by the principal components.
) decreases orthogonal to the subspace spanned by the principal components.



Next: 2.2 Vector quantization
Up: 2.1 Principal component analysis
Previous: 2.1.1 Neural networks for
Heiko Hoffmann
2005-03-22
![]() (Tipping and Bishop, 1997). The given set
{
(Tipping and Bishop, 1997). The given set
{![]() } is assumed to originate from a probability density
p(
} is assumed to originate from a probability density
p(![]() ). Further,
). Further, ![]() is assumed to be a linear combination of a vector
is assumed to be a linear combination of a vector
![]()
![]() IRq with density
p(
IRq with density
p(![]() ) and a noise vector
) and a noise vector
![]()
![]() IRd with density
p(
IRd with density
p(![]() ),
),
![]() are the eigenvectors of the covariance matrix of
{
are the eigenvectors of the covariance matrix of
{![]() }; the diagonal matrix
}; the diagonal matrix
![]() contains the corresponding eigenvalues, and
contains the corresponding eigenvalues, and ![]() is an arbitrary rotational matrix (note,
is an arbitrary rotational matrix (note, ![]() has a uniform Gaussian distribution). The noise variance
has a uniform Gaussian distribution). The noise variance ![]() turns out to be the residual variance per dimension,
turns out to be the residual variance per dimension,